Excel-Varianzberechnung: Eine Anleitung mit Beispielen
Die Varianz ist ein statistisches Maß, das uns zeigt, wie stark eine Reihe von Zahlen gestreut ist. Es ist ein entscheidendes Konzept in der Finanzwelt, in der Wissenschaft und vielen anderen Bereichen und hilft uns zu verstehen, wie stark die Variabilität oder Streuung innerhalb unserer Datensätze ist. Excel bietet eine einfache Möglichkeit, die Varianz zu berechnen, was sowohl für Anfänger als auch für fortgeschrittene Benutzer zugänglich ist. In diesem Artikel werden wir untersuchen, wie dies mit klaren Beispielen funktioniert.
Was ist Varianz?
Einführung in Excel-Varianzfunktionen
Wie berechnet man die Varianz in Excel?
- VAR.S vs VAR.P – Berechnung der Varianz aus einer Stichprobe oder Population
- VAR.S vs VARA – Berechnung der Varianz einschließlich oder ausschließlich Texte und logische Werte
Varianz vs Standardabweichung
Was ist Varianz?
Varianz ist ein statistischer Begriff, der beschreibt, inwieweit die Zahlen in einem Datensatz vom Mittelwert oder Durchschnitt der Zahlen abweichen. Im Wesentlichen misst sie, wie weit die Zahlen gestreut sind. Ein wichtiger Punkt beim Verständnis der Varianz ist die Erkenntnis, dass sie den Grad der Variation oder Streuung innerhalb einer Reihe von Werten quantifiziert. Eine hohe Varianz zeigt an, dass die Zahlen weit gestreut sind; eine niedrige Varianz deutet darauf hin, dass sie eng um den Mittelwert gruppiert sind.
Ein einfaches Beispiel zur Veranschaulichung der Varianz:
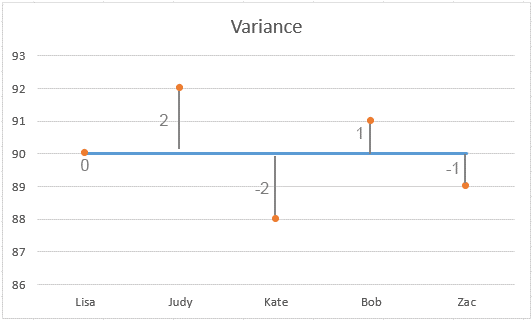
Szenario: Betrachten Sie eine Klasse mit fünf Schülern und ihren Ergebnissen in einem Mathetest von 100 Punkten. Die Ergebnisse sind 90, 92, 88, 91 und 89.
Berechnen des Mittelwerts: Zuerst berechnen wir den Durchschnitt (Mittelwert). Der Mittelwert ist
Berechnen der Varianz: Dann berechnen wir die Varianz. Dies beinhaltet das Subtrahieren des Mittelwerts von jedem Ergebnis, das Quadrieren des Ergebnisses und anschließend das Mitteln dieser quadrierten Differenzen.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
Ein Diagramm zeigte die Streuung der Ergebnisse:
Verständnis des Ergebnisses:
Niedrige Varianz: In diesem Beispiel beträgt die Varianz 2. Dies ist relativ niedrig, was zeigt, dass die meisten Ergebnisse nahe am Mittelwert (90) liegen. Je niedriger die Varianz, desto näher liegen die einzelnen Zahlen im Datensatz am Mittelwert.
Null Varianz: Wenn alle Schüler genau 90 Punkte erreicht hätten, wäre die Varianz 0, was auf keinerlei Variabilität hindeutet. Jedes Ergebnis wäre identisch.
Hohe Varianz: Umgekehrt würde eine höhere Varianz anzeigen, dass die Ergebnisse weiter vom Mittelwert gestreut sind, was eine größere Variabilität in der Leistung der Schüler zeigt.
Zusammengefasst gibt die Varianz uns einen numerischen Wert, der hilft zu quantifizieren, wie sehr die Ergebnisse (oder jede Reihe von Zahlen) vom Durchschnittswert abweichen und bietet Einblicke in die Konsistenz oder Variabilität der Daten.
Einführung in Excel-Varianzfunktionen
Excel bietet mehrere Funktionen zur Berechnung der Varianz, die jeweils für unterschiedliche Datenszenarien entwickelt wurden.
Das Verständnis dieser Funktionen ist entscheidend für eine genaue statistische Analyse.
VAR.S (Stichprobenvarianz, nur Zahlen):
- Berechnet die Varianz basierend auf einer Stichprobe der Grundgesamtheit.
- Am besten geeignet, wenn eine Teilmenge der Daten analysiert wird, um Rückschlüsse auf das Ganze zu ziehen.
VAR.P (Populationsvarianz, nur Zahlen):
- Berechnet die Varianz für die gesamte Grundgesamtheit.
- Ideal, wenn Sie über vollständige Daten verfügen und nicht nur über eine Stichprobe.
VARA (Stichprobenvarianz, einschließlich Text und Logikwerte):
- Ähnlich wie VAR.S, aber schließt Text und logische Werte in die Berechnung ein (Text wird als 0 behandelt, WAHR als 1, FALSCH als 0).
- Nützlich, wenn Ihr Datensatz gemischte Typen enthält (Zahlen, Text und logische Werte).
VARPA (Populationsvarianz, einschließlich Text und Logikwerte):
- Die Populationsvarianz-Version von VARA.
- Schließt alle Arten von Daten in die Varianzberechnung für die gesamte Grundgesamtheit ein.
VAR (Legacy-Stichprobenvarianz):
- Eine ältere Version von VAR.S, hauptsächlich in Excel 2007 und früher verwendet.
- Es wird empfohlen, VAR.S in neueren Versionen für Konsistenz und Klarheit zu verwenden.
VARP (Legacy-Populationsvarianz):
- Die ältere Version von VAR.P.
- Wie bei VAR wird empfohlen, VAR.P in neueren Excel-Versionen zu verwenden.
Unterschiede und Vergleiche:
- Stichprobe vs. Grundgesamtheit: VAR.S und VARA sind für Stichproben, während VAR.P und VARPA für die gesamte Grundgesamtheit gedacht sind.
- Datentyp-Berücksichtigung: VARA und VARPA schließen Text und logische Werte in die Berechnung ein, im Gegensatz zu VAR.S und VAR.P.
- Legacy vs. Moderne Funktionen: VAR und VARP sind ältere Funktionen und können durch VAR.S und VAR.P für eine bessere Kompatibilität mit aktuellen Excel-Versionen ersetzt werden.
Vergleichstabelle:
| Funktion | Berücksichtigter Datentyp | Grundgesamtheit oder Stichprobe | Anwendungsfall |
| VAR.S | Nur Zahlen | Stichprobe | Stichprobenvarianz für numerische Daten |
| VAR.P | Nur Zahlen | Grundgesamtheit | Populationsvarianz für Zahlen |
| VARA | Zahlen, Text, Logikwerte | Stichprobe | Stichprobenvarianz für gemischte Daten |
| VARPA | Zahlen, Text, Logikwerte | Grundgesamtheit | Populationsvarianz für gemischte Daten |
| VAR | Nur Zahlen | Stichprobe | Legacy-Funktion für Stichprobenvarianz |
| VARP | Nur Zahlen | Grundgesamtheit | Legacy-Funktion für populär |

Entfesseln Sie die Magie von Excel mit Kutools AI
- Intelligente Ausführung: Führen Sie Zellenoperationen durch, analysieren Sie Daten und erstellen Sie Diagramme – alles angetrieben durch einfache Befehle.
- Benutzerdefinierte Formeln: Erstellen Sie maßgeschneiderte Formeln, um Ihre Arbeitsabläufe zu optimieren.
- VBA-Codierung: Schreiben und implementieren Sie VBA-Code mühelos.
- Formelinterpretation: Verstehen Sie komplexe Formeln mit Leichtigkeit.
- Textübersetzung: Überwinden Sie Sprachbarrieren in Ihren Tabellen.
Wie berechnet man die Varianz in Excel?
In diesem Abschnitt werden wir zwei Beispiele bereitstellen, um zu demonstrieren, wie man die Varianz in Excel berechnet und die Unterschiede zwischen verschiedenen Varianzfunktionen erklärt. Als Ergebnis werden Sie sehen, dass verschiedene Varianzfunktionen völlig unterschiedliche Ergebnisse für dieselben Beispieldaten liefern.
VAR.S vs VAR.P – Berechnung der Varianz aus einer Stichprobe oder Grundgesamtheit
Szenario: Berechnung der Varianz für eine kleine Stichprobe einer Grundgesamtheit im Vergleich zur gesamten Grundgesamtheit.
Beispiel: Berechnen Sie die Varianz für die Werte in Spalte A2:A12.
Formel: Wählen Sie eine leere Zelle aus und geben Sie je nach Bedarf eine der folgenden Formeln ein, dann drücken Sie die Eingabetaste.
Erhalten der Varianzen für die Stichprobe eines großen Datensatzes (angenommen, die Werte in A2:A12 sind Teile eines großen Datensatzes)
=VAR.S(A2:A12)
Erhalten der Varianz für die gesamte Grundgesamtheit (angenommen, die Werte in A2:A12 sind der gesamte Datensatz)
=VAR.P(A2:A12)
Wie Sie sehen, führen gleiche Werte aber unterschiedliche Varianzfunktionen zu unterschiedlichen Ergebnissen.
Warum unterscheiden sich die Ergebnisse von VAR.S und VAR.P?
- VAR.S: Diese Funktion wird verwendet, wenn Ihr Datensatz eine Stichprobe aus einer größeren Grundgesamtheit darstellt. Sie berechnet die Varianz basierend auf der „n-1“-Methode, wobei „n“ die Anzahl der Datenpunkte in der Stichprobe ist. Die Verwendung von „n-1“ anstelle von „n“ als Nenner korrigiert die Verzerrung in der Stichprobe und macht sie zu einem unverzerrten Schätzer der Populationsvarianz. Sie liefert eine Schätzung, wie die Daten in der Stichprobe um den Stichprobenmittelwert variieren.
- VAR.P: Diese Funktion wird verwendet, wenn Ihr Datensatz eine gesamte Grundgesamtheit und nicht nur eine Stichprobe davon darstellt. Sie berechnet die Varianz basierend auf der „n“-Methode, wobei „n“ die Anzahl der Datenpunkte in der Grundgesamtheit ist. Sie geht davon aus, dass der Datensatz die gesamte Grundgesamtheit abdeckt, sodass keine Korrektur der Verzerrung wie bei VAR.S notwendig ist.
- Zusammengefasst besteht der Hauptunterschied im Nenner der Formel. VAR.S verwendet „n-1“, um die Stichprobennatur der Daten zu berücksichtigen, während VAR.P „n“ für Populationsdaten verwendet, bei denen keine Stichprobenziehung beteiligt ist. Abhängig von Ihrem Datensatz und ob es sich um eine Stichprobe oder eine vollständige Grundgesamtheit handelt, sollten Sie die entsprechende Funktion zur Berechnung der Varianz auswählen.
VAR.S vs VARA – Berechnung der Varianz einschließlich oder ausschließlich Texte und logische Werte
Szenario: Entscheidung, ob logische Werte und Texte in die Varianzberechnung einbezogen werden sollen.
Beispiel: Berechnen Sie die Varianz für die Werte in Spalte A2:A12.
Formel: Wählen Sie eine leere Zelle aus und geben Sie je nach Bedarf eine der folgenden Formeln ein, dann drücken Sie die Eingabetaste.
Erhalten der Varianzen für die Stichprobe eines großen Datensatzes unter Ignorierung von Texten und logischen Werten.
=VAR.S(A2:A12)
Erhalten der Varianz für die Stichprobe eines großen Datensatzes einschließlich Texte und logische Werte.
=VARA(A2:A12)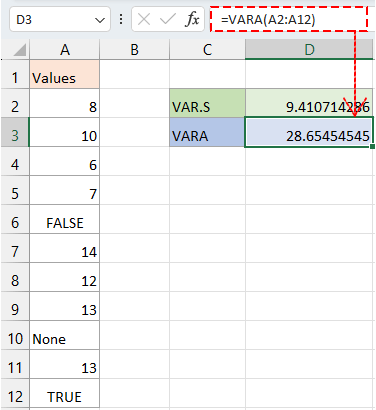
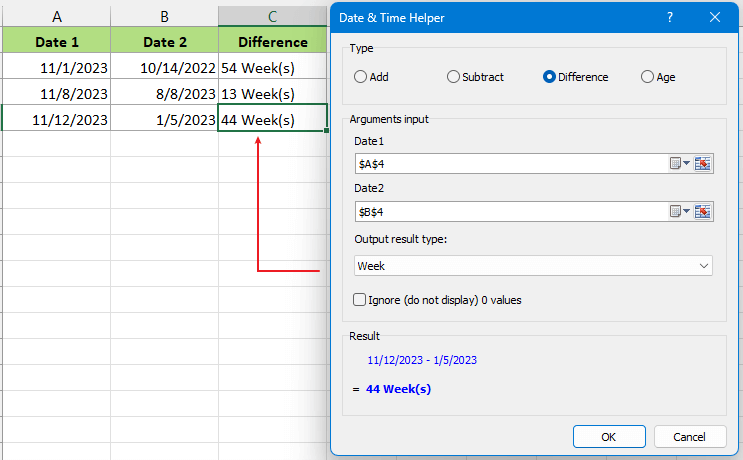
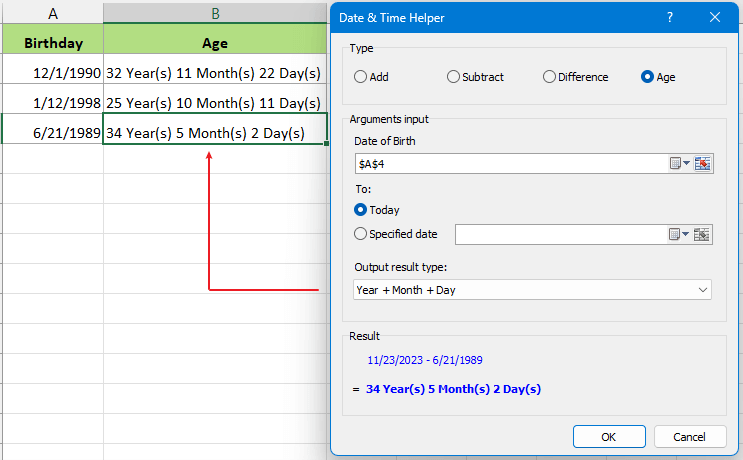
Machen Sie Datums- und Zeitberechnungen fliegend
Kutools for Excel's Date Time Helper ist ein unglaublich effizientes Tool, das komplexe Datums- und Zeitberechnungen vereinfacht. Probieren Sie es aus und sehen Sie, wie es Ihre Datenverwaltungserfahrung transformiert!
Varianz vs Standardabweichung
Ähnlichkeiten:
Maß für die Streuung:
Sowohl Varianz als auch Standardabweichung sind statistische Maße, die verwendet werden, um die Streuung oder Dispersion innerhalb eines Datensatzes zu beschreiben. Sie quantifizieren, wie weit die einzelnen Zahlen im Datensatz vom Mittelwert (Durchschnitt) abweichen.
Datenanalyse:
Beide werden häufig in der statistischen Analyse verwendet, um die Datenvariabilität zu verstehen. Sie sind in Bereichen wie Finanzen, Forschung, Qualitätskontrolle und mehr unerlässlich.
Aus dem Mittelwert berechnet:
Die Berechnung von Varianz und Standardabweichung beginnt mit dem Mittelwert des Datensatzes. Sie bewerten die Variabilität in Bezug auf diesen zentralen Wert.
Unterschiede:
Maßeinheiten:
Varianz: Quadrierte Einheiten der Originaldaten. Zum Beispiel, wenn die Daten in Metern vorliegen, wird die Varianz in Quadratmetern angegeben.
Standardabweichung: Gleiche Einheiten wie die Originaldaten. Fortsetzend das Beispiel, wenn die Daten in Metern vorliegen, wird die Standardabweichung ebenfalls in Metern angegeben.
Interpretation:
Varianz: Liefert eine quadrierte Schätzung, die weniger intuitiv zu interpretieren ist, da sie nicht in derselben Skala wie die Originaldaten vorliegt.
Standardabweichung: Einfacher zu interpretieren, da sie in denselben Einheiten wie die Daten vorliegt. Sie zeigt die durchschnittliche Entfernung der Datenpunkte vom Mittelwert an.
Mathematische Definition:
Varianz: Der Durchschnitt der quadrierten Differenzen vom Mittelwert.
Standardabweichung: Die Quadratwurzel der Varianz.
Empfindlichkeit gegenüber Extremwerten:
Varianz: Empfindlicher gegenüber Ausreißern, da sie die Differenzen quadriert.
Standardabweichung: Obwohl von Ausreißern beeinflusst, ist sie im Vergleich zur Varianz aufgrund der Quadratwurzel weniger empfindlich.
Anwendungen:
Varianz:
Wird verwendet, wenn der Fokus auf der quadrierten Größe der Streuung liegt.
Nützlich in statistischen Modellen und Berechnungen, wo das Quadrieren notwendig ist, um negative Werte zu eliminieren.
Oft in Finanzmodellen zur Risikobewertung verwendet, da sie Volatilität misst.
Standardabweichung:
Wird häufiger in Berichten und täglichen Anwendungen verwendet, aufgrund ihrer direkten Beziehung zur Datenskala.
Unverzichtbar in empirischer Forschung, um die Variabilität zu verstehen.
Häufig in der Qualitätskontrolle, Wetterberichten und Standardwerten in Tests verwendet.
Fazit:
Während Varianz und Standardabweichung beide dazu dienen, die Streuung eines Datensatzes zu messen, unterscheiden sich ihre Anwendungen aufgrund ihrer Maßeinheiten und Interpretierbarkeit. Die Standardabweichung, mit ihrer direkten Beziehung zur Skala der Daten, ist tendenziell benutzerfreundlicher, insbesondere in praktischen, alltäglichen Kontexten. Die Varianz hingegen ist oft besser für mathematische und statistische Modelle geeignet.
Diese Übersicht und dieser Vergleich sollten ein klares Verständnis darüber vermitteln, wann und warum man jede Varianzfunktion in Excel verwendet, was eine genauere und sinnvollere Datenanalyse ermöglicht. Für weitere bahnbrechende Excel-Strategien, die Ihre Datenverwaltung verbessern können, erkunden Sie hier weitere Informationen.
Die besten Office-Produktivitätstools
Kutools für Excel - Hilft Ihnen, sich von der Masse abzuheben
Kutools für Excel bietet über 300 Funktionen, sodass alles, was Sie benötigen, nur einen Klick entfernt ist...
Office Tab - Aktivieren Sie tabbed Lesen und Bearbeiten in Microsoft Office (inklusive Excel)
- In einer Sekunde zwischen Dutzenden offener Dokumente wechseln!
- Reduziert Hunderte von Mausklicks für Sie jeden Tag, verabschieden Sie sich von der Maushand.
- Steigert Ihre Produktivität um 50 % beim Anzeigen und Bearbeiten mehrerer Dokumente.
- Bringt Effiziente Tabs ins Office (inklusive Excel), genau wie bei Chrome, Edge und Firefox.
Inhaltsverzeichnis
- Was ist Varianz?
- Einführung in Excel-Varianzfunktionen
- Wie berechnet man die Varianz in Excel?
- VAR.S vs VAR.P – Berechnung der Varianz aus einer Stichprobe oder Grundgesamtheit
- VAR.S vs VARA – Berechnung der Varianz einschließlich oder ausschließlich Texte und logische Werte
- Varianz vs Standardabweichung
- Verwandte Artikel
- Beste Office-Produktivitätstools
- Kommentare